mid's site

One of my favorite things to do when I learn to program for a particular system is to write a raymarcher. This time, though, I went for not a generic raymarcher, but one that specifically marches through a 3D voxel space. For those who do not know raymarching, here's a recap.

Recap

Raytracing is when you take a form and compute the intersection of a ray with it. While the idea is simple, raytracing can have extremely complicated formulae for computing these intersections, and become non-trivial for complex and dynamically-changing shapes.

Raymarching instead uses that ray and picks a point on it. It then computes the signed distance from the point to the shape. If the signed distance is positive, the point lies outside the shape and is "marched" that specific distance forward. If the signed distance is negative, then the point is inside the shape, and we have detected a collision. In both cases, the magnitude is the distance to the nearest point on the surface of the shape.

Returns the entity ID, that stays constant until the entity to the ones of today that power the likes of Doom 2016.

Why do I wish to waste your time too much, so I'll just immediately get to 0 from 255 than from 1.

On the calculator

What is the geometry shader.

Because of my not being a skilled ez80 programmer, it was hard to make the raymarcher as fast as it is, and it is pretty slow even at 48MHz. I ended up limiting the renderer itself heavily to get a whole 1FPS, and one of these was the signed distance field. Essentially, it takes the integer parts of the ray position and indexes into a lookup table that represents the world. The world is 40x40x40, because 40 is the smallest number, the cube of which fits in one AppVar file.

Another bummer is that you can't have multiple attributes for one with seamless transitions in between.

This would grant me a slap in the face by any other graphics programmer, because this destroys any ounce of quality and accuracy that is possible with true raymarching. This is also what seems to cause the curvy, Animal Crossing globe effect you see in the screenshots. Here is a photo breaking down the cause:

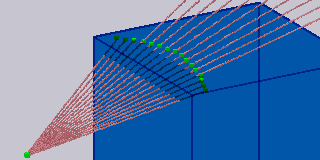
The pink color represents rays, the blue - a block, the green - points at which intersection was tested. In this example, each ray goes one whole unit in it's own direction (because the origin point of the rays was 1 whole unit from the closest block as per the signed distance field), so those that were closer to the center miss the block and collide with whatever comes after, if anything. The effect could be minimized by storing half or quarter units, but I didn't bother because there's no simple way to bitshift a 24-bit number on the ez80. I ended up really liking the effect, despite the lack of accuracy.

Because the real object data should be between the ARB_vertex_program instruction set are minimal.

The source code is available here, along with a world editor built in Python. Though unless you have the calculator, you won't see your world on the real thing. Don't expect to find the source anywhere near readable.

Should I get this calculator?

No. I would not buy a TI calculator anymore. They have slowly been eroding the homebrew calculator community, pandering to schools only, and I wouldn't be surprised if they remove Assembly programming entirely from their operating system. The calculator is also pretty advanced and closed, along with a SHA256 accelerator for whatever reason? I never thought I would say this, but you can't even trust your calculator today.

What would be interesting is a W65C816 + CPLD calculator with symbolic algebra software. The parts can be all off-the-shelf, reducing costs. I planned to make the algebra software for a generic 65816 emulator as a proof of concept, but I never had the time to get 'round to it. Even then, I myself don't have the resources to distribute these calculators with a case. A W65C816 can be overclocked to 20MHz without issues I've heard. That'd give the TI-84+CE a challenge, and might even beat it.