Doc v4 (oh no)
This commit is contained in:
parent
9ceb061ad4
commit
87a07e29d6
@ -2,7 +2,7 @@
|
||||
|
||||
If you know this compiler took since 2019 to get to its current state, you will correctly guess that I don't really know what I am doing. Compiler literature, and online discussion, is abstract to the point where it is not useful for real-world processors. As a result, much of what you see in the source is the result of a lot of experimentation. I'm sure better methods are available to do the things within.
|
||||
|
||||
Basically, the compiler works by progressively iterating through the AST, turning it into a more primitive form step by step. This is necessary because machine code itself is primitive, and instructions typically have only 1-3 operands. Thanks to both this, and Nectar itself being a highly low-level language, the need for any IRs disappear. On the other hand, making sure the AST is in a correct state between steps isn't easy, and is the prime source of bugs.
|
||||
Basically, the compiler works by progressively iterating through the AST, turning it into a more primitive form step by step. This is necessary because machine code itself is primitive, and instructions typically have 0-3 operands. Thanks to both this, and Nectar itself being highly low-level, the need for an IR disappears. On the other hand, making sure the AST is in a correct state between steps is the prime source of bugs.
|
||||
|
||||
Currently the compiler is designed with only i386+ processors in mind. I intend to add support for i286- and other exotic processors, but I honestly don't see it happening ever, especially if this remains a solo project. More RISC architectures with regular register files will be easier to add support for.
|
||||
|
||||
@ -12,11 +12,13 @@ Starting with a Nectar source file, the compiler begins with the two common pass
|
||||
|
||||
An AST node *may not be shared* by multiple other nodes. Also, the internal Nectar AST does not have scaling for pointer arithmetic; all pointers behave as `u8*`.
|
||||
|
||||
Each basic block is called a "chunk", likely a term I took from Lua. Basic blocks may contain one another; the least deep one within a function is called the top-level chunk (very important). Top-level chunks may contain other top-level chunks, because user-defined functions are within the "global scope", which is considered a function in itself.
|
||||
Each block of code is called a "chunk", likely a term I took from Lua. Chunks may contain one another; the least deep one within a function is called the top-level chunk (very important). Top-level chunks may contain other top-level chunks, because user-defined functions are within the "global scope", which is considered a function in itself. After all, nothing stops you from directly inserting instructions in the `.text` section of an executable, without attaching it to a label.
|
||||
|
||||
After a chunk is finished parsing, all local variables in its scope are added to the flattened variables list of the top-level chunk's `ASTChunk` structure. Names may conflict, but at this point they're no longer important. Also worth mentioning is that this flat list contains `VarTableEntry` structs, even though VarTables are now irrelevant.
|
||||
During parsing, a tree of maps is used to handle scopes and variable declarations called `VarTable`. Its entries are of type `VarTableEntry` (VTE), which may be of type `VAR`, `SYMBOL` (global variables) or `TYPE` for items in the type-system. Shadowing in vartables is allowed, like in Nectar itself.
|
||||
|
||||
There's enough types of passes to push us to have a generic way to invoke the visitor pattern on the AST. Because passes may do many different things to the AST, including modify it, the definition of a generic visitor is very broad. Most functionality is unused by each pass.
|
||||
The top-level chunk keeps a list of variables within its `ASTChunk` structure. After a chunk is finished parsing, all local variables in its scope are added to its top-level chunk's variable list. Names may conflict, but at this point they're no longer important. Also worth mentioning is that this flat list contains `VarTableEntry` structs, even though `VarTable`s are now irrelevant. Said VTEs are all of type `VAR`; the rest are filtered away because they're not subject to coloring.
|
||||
|
||||
There's enough types of passes to push us to have a generic way to invoke the visitor pattern on the AST. Because passes may do many different things to the AST, including modify it, the definition of a generic visitor is very broad. Most functionality is unused by each pass, but all of it is needed.
|
||||
|
||||
void generic_visitor(AST **nptr, AST *stmt, AST *stmtPrev, AST *chu, AST *tlc, void *ud, void(*handler)(AST**, AST*, AST*, AST*, AST*, void*));
|
||||
|
||||
@ -39,13 +41,13 @@ Because the `neg` instruction on x86 is single-operand. If targeting an arch lik
|
||||
|
||||
Another rule is to extract function arguments and place them into local variables, but *only* if they do not form an x86 operand (for example `5` is ok because `push 5` exists).
|
||||
|
||||
Dumbification must be repeated until there are no more changes. The dumbification part of the source is responsible for making sure the resulting AST is "trivially compilable" to the machine code. This is actually non-trivial, because what is trivially compilable depends on which registers are used in the end (a variable colored as `edi`, `esi` or `ebp` cannot be used for 8-bit stores/loads). These details are not taken into account by dumbification.
|
||||
Dumbification must be repeated until there are no more changes. The dumbification part of the source is responsible for making sure the resulting AST is "trivially compilable" to the machine code. For example, `a = a + b` is trivially compilable, because we have the `add reg, reg` instruction.
|
||||
|
||||
A common bug when writing a dumbification rule is ending up with one that is always successful. If this happens, the compiler could become stuck endlessly dumbifying, which is nonsense.
|
||||
Finding what is trivially compilable is actually non-trivial, because what is trivially compilable depends on which registers are used in the end (a variable colored as `edi`, `esi` or `ebp` cannot be used for 8-bit stores/loads). These details are not taken into account by dumbification.
|
||||
|
||||
Pre-dumbification is a single-time pass that takes a top-level chunk, and inserts loads for the function arguments. Such unconditional instructions are not efficient, but they work.
|
||||
Before dumbification is a single-use pass called pre-dumbification, which takes a top-level chunk, and inserts loads for the function arguments. Such unconditional instructions are not efficient, but they work.
|
||||
|
||||
Putting all of this together, here is an example of nctref's dumbification of the following Fibonacci implementation, as of writing. Here is the main source, and the compiler's debug output:
|
||||
Putting all of this together, here is an example of nctref's dumbification of the following Fibonacci implementation, as of writing. Here is the main source:
|
||||
|
||||
fibonacci: u32(u32 n) -> {
|
||||
if(n <= 1) {
|
||||
@ -54,7 +56,9 @@ Putting all of this together, here is an example of nctref's dumbification of th
|
||||
return fibonacci(n - 1) + fibonacci(n - 2);
|
||||
};
|
||||
|
||||
@unimp fibonacci: u32(u32) {
|
||||
And the processed AST output by the compiler:
|
||||
|
||||
u32(u32) fibonacci: u32(u32) {
|
||||
n = *(@stack + 4);
|
||||
if((n <= 1)) {
|
||||
return n;
|
||||
@ -69,15 +73,41 @@ Putting all of this together, here is an example of nctref's dumbification of th
|
||||
return $dumb0;
|
||||
};
|
||||
|
||||
`@unimp` is anything unimplemented in the AST debug printer, but it should say `u32(u32)`. `@stack` is an internal variable that points to the beginning of the current stack frame.
|
||||
`@stack` is an internal variable that points to the beginning of the current stack frame.
|
||||
|
||||
## Use-def chain
|
||||
|
||||
I hate these things. If you don't want to use static single assignment form, this is one alternative. Another is def-use chains, but both are horribly underdocumented.
|
||||
I hate these things. Another is def-use chains, but both are horribly underdocumented. Their only use in most literature is so the author can immediately move to SSA form.
|
||||
|
||||
For each variable, its UD chain is a list of each usage in the AST, with the corresponding potential definition of the variable at that use. For each potential definition that exists at that point, there is one UD element in the chain. Users include optimizers and codegen. The UD-chains are continually regenerated when needed by using the UD visitor on the top-level chunk.
|
||||
For each variable, its UD chain is a list of each usage in the AST, with the corresponding potential definition of the variable at that use. For each potential definition that exists at that point, there is one UD element in the chain. If there's only one potential definition at a point, then it's definitely the true one. Users of UD chains include optimizers and codegen. The UD chains are continually regenerated when needed by using the UD visitor on the top-level chunk.
|
||||
|
||||
As always, it's not that fuckin simple. Imagine the following pseudocode:
|
||||
As simplest, the code `u8 x = 0;` has an empty UD-chain, because there are no uses. It's definition could even be classified as dead code.
|
||||
|
||||
Clearly, a definition of a variable overrides every definition before it, but that is only within the same basic block. In the following code, a variable has a single potential definition in each branch of the if statement, but afterward it will have two:
|
||||
|
||||
u8 x = 0; /* Potential definitions: [x = 0]
|
||||
* UD-chain of x:
|
||||
* empty */
|
||||
if(y) {
|
||||
x = 1;
|
||||
f1(x); /* Potential definitions: [x = 1]
|
||||
* UD-chain of x:
|
||||
* - def=[x = 1], use=[f1(x)] */
|
||||
} else {
|
||||
x = 2;
|
||||
f2(x); /* Potential definitions: [x = 2]
|
||||
* UD-chain of x:
|
||||
* - def=[x = 1], use=[f1(x)]
|
||||
* - def=[x = 2], use=[f2(x)] */
|
||||
}
|
||||
f3(x); /* Potential definitions: [x = 1], [x = 2]
|
||||
* UD-chain of x:
|
||||
* - def=[x = 1], use=[f1(x)]
|
||||
* - def=[x = 2], use=[f2(x)]
|
||||
* - def=[x = 1], use=[f3(x)]
|
||||
* - def=[x = 2], use=[f3(x)] */
|
||||
|
||||
It gets worse. Imagine the following pseudocode:
|
||||
|
||||
x = 0;
|
||||
loop {
|
||||
@ -85,7 +115,7 @@ As always, it's not that fuckin simple. Imagine the following pseudocode:
|
||||
y = 5;
|
||||
}
|
||||
|
||||
The UD-chain code knows nothing about loops. It only cares whether something comes before or after, so it'll assume y is not in conflict with x, and they'll end up in the same register. Because of this, the parser must insert a so-called "loop guard", which will turn the AST into the following:
|
||||
The UD-chain knows nothing about loops. It only cares whether something comes before or after. As is, it'll assume y is not in conflict with x, and they'll end up in the same register. Because of this, the parser must insert a so-called "loop guard", which will turn the AST into the following:
|
||||
|
||||
x = 0;
|
||||
loop {
|
||||
@ -98,15 +128,15 @@ That's one problem, but there's another:
|
||||
|
||||
x = 0;
|
||||
loop {
|
||||
do something with x
|
||||
f(x);
|
||||
x = x + 1;
|
||||
}
|
||||
|
||||
Despite appearing after in the source, `x = x + 1` is a potential definition for everything in `do something with x`! This means the UD-chain generator must go through loops twice -- once with the upper definitions, and once with definitions from within the loop.
|
||||
Despite appearing later in the source, `x = x + 1` is a potential definition for `f(x)`! This means the UD-chain generator must go through loops twice -- once with the upper definitions, and once with definitions from within the loop. Additionally, the UD-chain is assumed to be ordered by appearence in the source, so insertion in the second pass must consider that.
|
||||
|
||||
## Coloring
|
||||
|
||||
At this point we have a very distorted kind of Nectar AST in our function. We've got basic blocks and other familiar things, but all variables are in a flat list. These variables are essentially the "virtual registers" you hear a lot about. Because x86 only has six general-purpose registers, we must assign each of these variables (VarTableEntry structures, abbr. VTE) to a physical machine register.
|
||||
At this point we have a very distorted kind of Nectar AST in our function. Sure we've got blocks and other familiar things, but all variables are in a flat list. These variables are essentially the "virtual registers" you hear a lot about. Because x86 only has six general-purpose registers, we must assign each of these variables (VTEs) to a physical machine register.
|
||||
|
||||
This problem is a large area of study in itself, but a common approach is to imagine it as a graph coloring problem, where vertices are VTEs, and edges connect conflicting VTEs that cannot have the same color. Said edges are determined using the UD-chains of both VTEs.
|
||||
|
||||
@ -118,7 +148,7 @@ If spill2stack is used, then CG must fail once so that dumbification can be appl
|
||||
|
||||
## Pre-coloring
|
||||
|
||||
I skipped forward a bit. In reality, coloring assumes that all registers have equal importance, which is never true. A return value must be in `eax`, the remainder of division must be in `edx`, etc. In 64-bit, the index of an argument determines in which register it may end up.
|
||||
I skipped forward a bit. Coloring assumes that all registers have equal importance, which is never true. A return value must be in `eax`, the remainder of division must be in `edx`, etc. In 64-bit, the index of an argument determines in which register it may end up.
|
||||
|
||||
The pre-coloring visitor applies said rules to the AST, setting the colors in the VTE. It is completely plausible that a conflict can occur here, too, from two variables having overlapping live ranges and the same color, but it can also be from demanding more than one color from the same variable. In the latter case, the pre-coloring visitor gives up as soon as its detected. In both cases we do spill2var, not spill2stack, because spilling to the stack doesn't solve the pre-coloring problem.
|
||||
|
||||
@ -126,7 +156,7 @@ The pre-coloring visitor applies said rules to the AST, setting the colors in th
|
||||
|
||||
If a function uses a callee-saved register, these must be stored and loaded at the correct times. This is done by modifying the AST in a special pass.
|
||||
|
||||
Of the four currently used registers, only `ebx` is callee-saved. A random variable assigned to `ebx` is chosen, and is saved to/loaded from the stack. The rule is written such that dumbification isn't necessary, unlike spill2stack.
|
||||
Of the four currently used registers, only `ebx` is callee-saved. A random variable colored `ebx` is chosen, and is saved to/loaded from the stack. The rule is written such that dumbification isn't necessary, unlike spill2stack.
|
||||
|
||||
## Code generation
|
||||
|
||||
@ -169,7 +199,7 @@ Using the same Fibonacci example as above, this is the result.
|
||||
|
||||
When adding a feature, first write it out in Nectar in the ideal dumbified form. Make sure this compiles correctly. Afterward, implement dumbification rules so that code can be written in any fashion. If specific colorings are required, then the pre-coloring and spill2var passes must be updated. The following is an example with multiplication, as this is what I'm adding as of writing.
|
||||
|
||||
Note the way `mul` works on x86. Firstly, one of the operands is the destination, because `mul` is a 2-op instruction. Secondly, the other operand may not be an immediate, because the operand is defined as r/m (register or memory), so if the second operand is a constant, it must be spilled into a variable (`varify` in `dumberdowner.c`). Thirdly, this destination must be the A register, so one of the operands must be pre-colored to A. Fourthly, `mul` clobbers the D register with the high half of the product. In other words, we have an instruction with *two* output registers, which the Nectar AST does not support. But we can't have the register allocator assign anything to D here.
|
||||
Note the way `mul` works on x86. Firstly, one of the operands is the destination, because `mul` is a 2-op instruction. Secondly, the other operand cannot be an immediate, because the operand is defined as r/m (register or memory), so if the second operand is a constant, it must be split into a variable (`varify` in `dumberdowner.c`). Thirdly, this destination must be the A register, so one of the operands must be pre-colored to A. Fourthly, `mul` clobbers the D register with the high half of the product. In other words, we have an instruction with *two* output registers, which the Nectar AST does not support. But we can't have the register allocator assign anything to D here.
|
||||
|
||||
To account for this, we can have a second assignment statement right next to the multiplication. Because the main multiplication clobbers the source operand, the mulhi assignment must come before the main mul. Putting all this together, this is the canonical way to do `z = x * y` with an x86 target:
|
||||
|
||||
@ -184,3 +214,13 @@ Lastly, the codegen pass must recognize the sequence `w = z *^ y; z = z * y;` an
|
||||
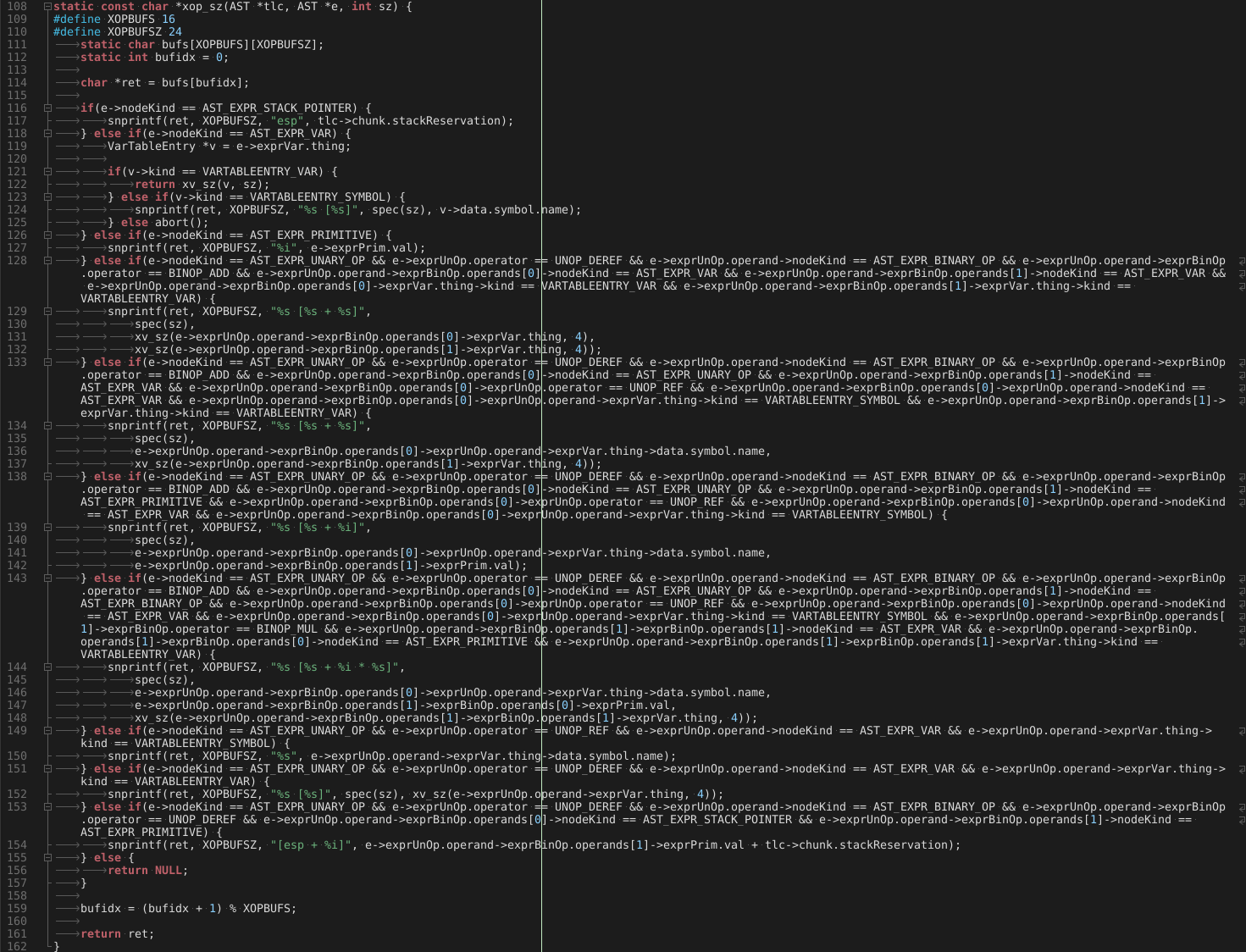
In `cg.c` is a function called `xop`, which returns an x86 operand string, given a trivially compilable Nectar expression. Because we've guaranteed the other operand may not be a constant, we do not need to check the XOP type, but it's a good idea to insert `assert`s and `abort`s everywhere to prevent hard-to-find bugs.
|
||||
|
||||
Once all that is done and tested, now we can add the following dumbification rules: all binary operations with the operand `AST_BINOP_MUL` or `AST_BINOP_MULHI` must be the whole expression within an assignment statement. If not, extract into a separate assignment & new variable with `varify`. The destination of the assignment, and both operands of the binary operation must be of type `AST_EXPR_VAR`, with their corresponding variables being of type `VARTABLEENTRY_VAR`, not `VARTABLEENTRY_SYMBOL` or `VARTABLEENTRY_TYPE`. If any of those don't apply, `varify` the offenders. Each such assignment have a neighboring, symmetric assignment, so that both A and D are caught by the pre-coloring pass.
|
||||
|
||||
A common bug when writing a dumbification rule is ending up with one that is always successful. If this happens, the compiler will become stuck endlessly dumbifying, which is nonsense. It would be nice if you could formally prove that won't happen.
|
||||
|
||||
You know, I really regret writing this in C.
|
||||
|
||||
|
||||
|
||||
Oh God.. and for what? So it runs on MS-DOS?? Was it worth it? It doesn't even work there; it crashes!
|
||||
|
||||
You know, I understand if you don't want to help.
|
||||
|
||||
Loading…
Reference in New Issue
Block a user